« Back Lapua Ballistics Tips: Stability Estimation
Some basics about bullet accuracy and stability estimation
Stability is an essential part of bullet accuracy. Stability is affected by several factors, the most important factors being barrel twist rate and the length of the projectile. To a lesser degree it is also affected by the bullet shape, velocity and environmental conditions. You can estimate bullet stability during the flight path with the stability estimator function in Lapua Ballistics. In this article, we will explain bullet stability to a high detail and how to use Lapua Ballistics as a tool to understand it.
What is barrel twist rate?
Twist rate is defined as the length of one full turn of the bullet (360 degrees) in inches or millimeters in the barrel. E.g. 1:10” means that the bullet makes one full turn over the distance of 10 inches. You can measure the twist rate of your rifle barrel by marking e.g. a cleaning rod with a flag made of adhesive tape, and measuring the distance where the flag rotates 360 degrees. Make sure that the cleaning rod follows exactly the lands in the barrel.
What happens if the bullet is too long compared to the twist rate?
If the bullet is too long compared to the twist rate, it will be unstable and may start to wobble or even turn completely crosswise. For the shooter, this translates as poor accuracy and oval or ”keyhole” shaped holes in the paper target. An overstabilized projectile does not follow exactly the trajectory of the curved flight path but flies slightly nose up. Technically speaking, the axis of the bullet does not follow the tangent of the trajectory. This increases the air drag and shortens the flight range. An unnecessary high rotation speed also intensifies the adverse effect of smaller shape and symmetry defects of the projectile.

How to increase bullet stability
The stability of a bullet can be increased by the following factors (roughly in the order of importance):
- Tighter (shorter) twist rate of the barrel
- Shorter bullet
- High altitude (lower air density)
- High temperature (lower air density)
- Low air pressure (lower air density)
- High humidity (lower air density. Yes, water vapor is less dense than air!)
Lower air density means less aerodynamic forces affecting the bullet so it remains stable easier.
Stability estimation - the theory
Traditionally, bullet stability is estimated by using quite simple equations like the Miller and Greenhill equations. Lapua Ballistics estimates the bullet stability by using both dynamic stability ’Sd’ and gyroscopic stability ’Sg’ during the full bullet trajectory. The value of the stability calculator is more in comparing different combinations with each other (twist rate, bullet to be used, muzzle velocity, environmental conditions, etc.) than trying to say simply if a bullet is stable or unstable.
Gyroscopic stability Sg means the ability of a rotating object to resist the change of its rotating axis. Sg is quite easy to calculate and its value at the muzzle has to be absolutely over 1.0 for a bullet to be stable. In practice some safety margin is needed there so the recommended minimum value is 1.4. Values clearly over 2.0 are unnecessary high because an overstabilized bullet has higher air drag due to the ”nose up” flight position and is more critical to small imperfections in the bullet shape and symmetry. Gyroscopic stability increases with flight time/distance because the rotational speed of the bullet does not decrease as fast as the forward velocity.
Dynamic stability Sd means the ability of the bullet to decrease a wobbling motion caused by an internal or external effect. In a dynamically stable bullet, the wobbling decreases with the time/distance and in a dynamically unstable bullet the wobbling increases with the time. Sd is much more difficult to evaluate than Sg and it needs 6 DOF calculations. Lapua Ballistics is one of the very few ballistics software solutions that is capable of utilizing this and possibly the only one completely free of charge. Most software are capable of estimating stability only by Sg which is usually reasonable good enough for short distances but not to long distances and to the transonic region – where Sd is the main factor for stability. The vertical axis of the stability curve expresses Sg and the horizontal axis Sd. The favorable stability region is expressed as light blue but high quality bullets often retain the stability also in the dark blue region.
Dynamic stability is affected by e.g. the bullet length and shape and the positions and distance between the center of mass (cm) and the center of pressure (cp). The distance between cm and cp is very important because it defines the aerodynamic moment vector that tries to turn the bullet crosswise. Air density is also important, the stability is better in a higher altitude and warm weather. The grooves (made by the lands in the barrel) on the bullet surface slightly affect the dynamic stability and decelerate the rotating speed faster compared to a smooth surface. Dynamic stability is usually the problem only at long distances and in the transonic region.
Stability is not an ON/OFF phenomenon, so Sg and Sd basically describe the tendency or risk for unstability. For that reason the graph in Lapua Ballistics is not black and white but light/dark blue. The bullet can fly - and often does - fly stable and accurate also far inside the dark blue region. As a rule of thumb, we can say that at the later (number of 100 m/yds markers) and in the more upper direction the line exits the light blue region, the better the bullet can resist external forces trying to make the bullet wobble, meaning that the stability and accuracy potential is better.
How to read the stability calculator in Lapua Ballistics
Simple guide for ensuring bullet stability
- The target for the gyroscopic stability value Sg at the muzzle is between 1.4 and 1.8. Never go below 1.2 and avoid values clearly over 2.0. This is a good guide for both short range and long range bullets. For most shooters this is enough and in that case, you don’t have to worry about the dynamic stability Sd.
- When you shoot long (over 600 m/yds) and extremely long (over 1 km/mi) ranges, you also need to pay attention to the dynamic stability. The stability curve should turn as late as possible (no. of distance markers) and only a little to the left. If the curve turns 90 degrees to the left it means a higher risk of unstability than if the curve turns only 45 degrees to the left. The stability curve of high BC long range bullets always turn clearly to the left.
- Long and sharp-nosed VLD bullets (Very Low Drag) may be problematic in the transonic region. Shorter projectiles tackle this problem easier but on the other hand they reach the transonic region earlier because of a lower BC. Transonic region stability can be improved by a tighter twist rate but this may have other undesired effects to the accuracy in general.
Example of bullet stability estimation in Lapua Ballistics:
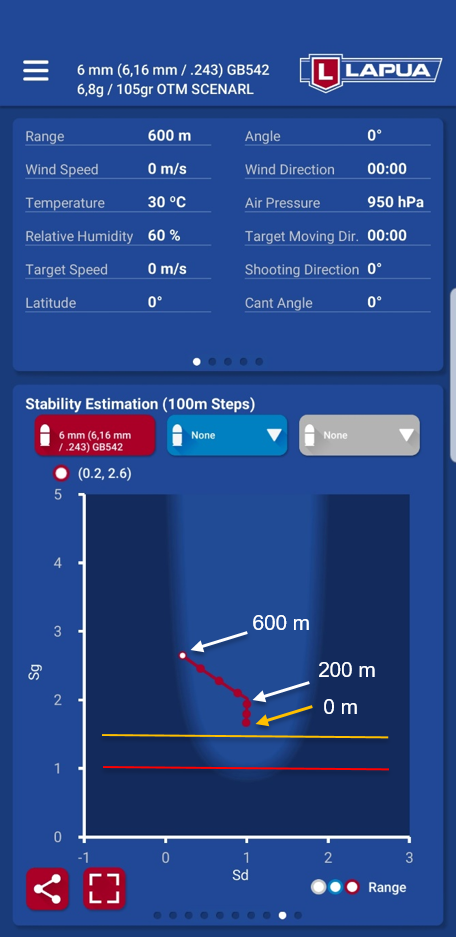
- Gyroscopic stability Sg is expressed on the y-axis (0 – 5).
- Dynamic stability Sd is expressed on the x-axis (-1 – +3).
- Maximum values are expressed also as numerical values in the top left corner (here Sd = 0,2 and Sg = 2,6).
- On the line, there are markers at each 100 m/yds starting from 0 m/yds but the line is actually calculated and shown in 10 m/yds intervals.
- The safe stability region is expressed as a light blue area. In the dark blue region the risk for unstability is increased but it doesn’t mean that the bullet is unstable. Only the bullet ability to correct external disturbances (e.g. flurry or transonic area disruption) is reduced.
- Gyroscopic stability at the muzzle (0 m/yds, first marker) should be at least over 1.0 (red line) and preferable over 1.4 (yellow line).
- Gyroscopic stability increases with the distance (here 1.7 -> 2.6) because the bullet retains its rotational speed better than forward velocity.
- Dynamic stability starts to weaken after 200 m/yds but in this case it is not dramatic and the bullet remains in the safe region up to 600 m/yds.
|
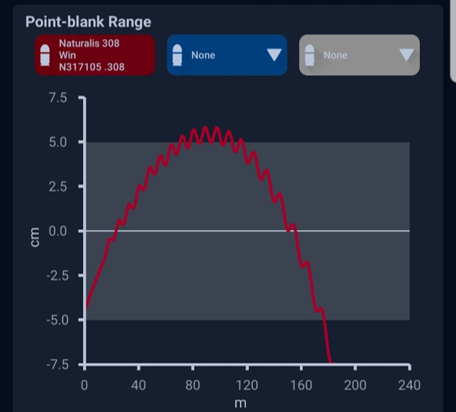
Effect of twist rate in .308 Win, example:
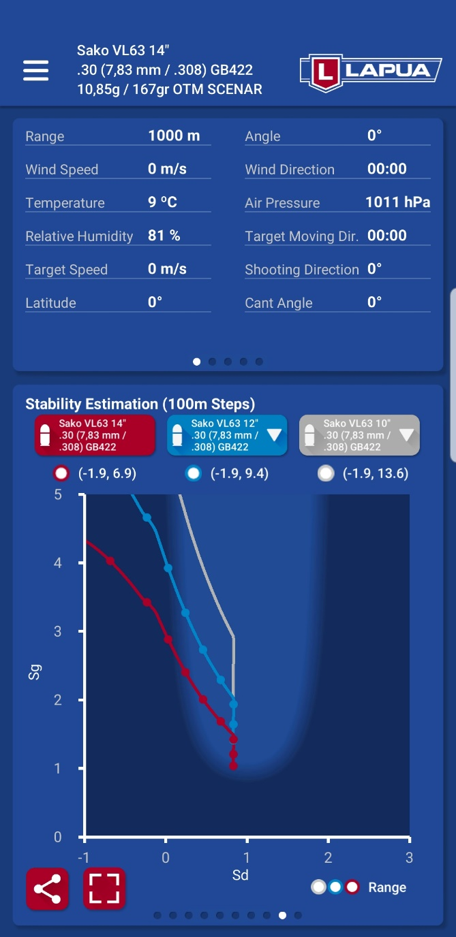
In this graph you can see the effect of the twist rate to gyroscopic and dynamic stability in a .308 Win. rifle with the 10,85 g / 167 gr GB422 Scenar bullet. This OTM bullet is mainly designed for short and medium ranges – up to about 600 m/yds.
- The 1:14” twist rate (red curve) is too slow (i.e. long) for this combination. Gyroscopic stability at the muzzle is too low (first red dot) ca. 1.0. There is a high risk for the bullet to be unstable already at the muzzle.
- The 1:12” twist rate (blue curve) is appropriate for this combination. Gyroscopic stability at the muzzle (first blue dot) is good, ca 1.4. The bullet travels the first 500 m/yds in a safe region and does not turn strongly left even after 500 m/yds. The bullet has good presumption to fly stable and accurate to long ranges.
- The 1:10” twist rate (gray curve) is slightly too fast for this combination. Gyroscopic stability at the muzzle (beginning of gray curve) is slightly too high, ca. 2.0, but the bullet likely works fine and shoots accurate. But the bullet is spinning unnecessary fast and may be susceptible to adverse effects of small imperfections in shape or symmetry. A good combination, but maybe not the optimal one.
- The exact Sg and Sd values can be seen in the trajectory table if Sg and Sd are selected as columns to be visible.
- Please note that the software may calculate the stability values for longer distances than the shooting distance so the last marker may not be the actual shooting distance.
- This feature is available only for Lapua bullets and cartridges because the details of bullet structures (e.g. moments of inertia, center of gravity, etc.) are not available for other bullets.
|
Effect of twist rate in .338 Lapua Magnum, example:
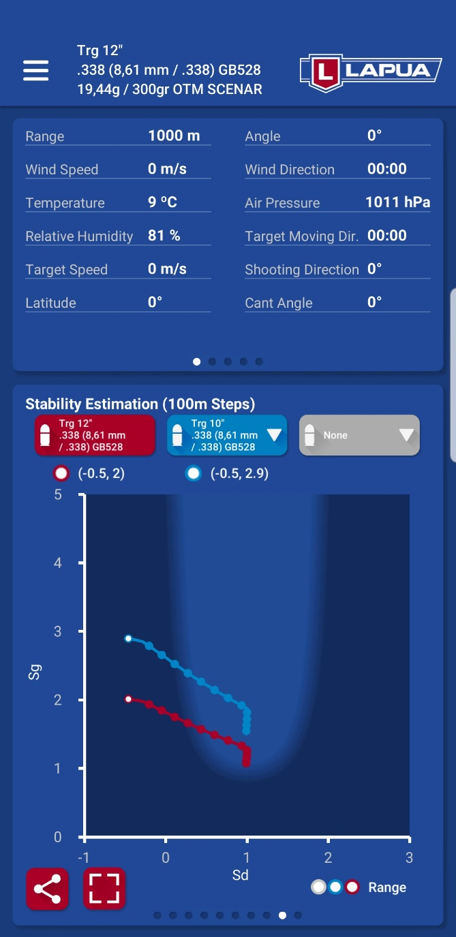
In this graph you can see the effect of twist rate to gyroscopic and dynamic stability in a .338 Lapua Magnum rifle with the 19,44 g / 300 gr GB528 Scenar OTM bullet.
- The 1:12” twist rate (red curve) is too slow (long) for this combination. Gyroscopic stability at the muzzle is too low (first red dot), ca. 1.0. There is a high risk for the bullet to be unstable already at the muzzle. This combination is known to be in the limit of appropriate function – sometimes it works, but usually not.
- The 1:10” twist rate (blue curve) is appropriate for this combination. Gyroscopic stability at the muzzle (first blue dot) is good, ca. 1.5. The bullet travels the first 800 m/yds in a safe region. Even when it exits the safe region at 800 m/yds, this bullet is well known for extremely good accuracy up to 1 500 m/yds and over. It is typical for all long high B.C. bullets that the Sd turns strongly to the left and exits the safe region.
|
How bullet length affects the stability
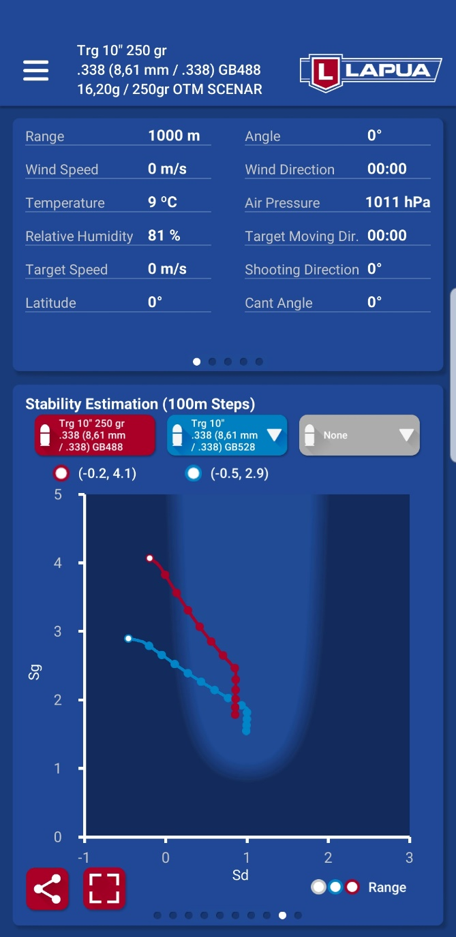
In this graph you can see the effect of bullet length to gyroscopic and dynamic stability in a .338 Lapua Magnum rifle with a 1:10” twist rate.
- The shorter 250 gr GB488 Scenar (red graph) retains its stability better than longer 300 gr GB528 Scenar (blue graph), but reaches the transonic region a little earlier than the ballistically better 300 gr bullet. You can compare differences in bullet velocity and energy in their respective graphs and trajectory table.
- If you can see a clear wave pattern in the trajectory curves, it is also an indication of potential instability. The most likely reason for this is a too slow (long) twist rate that doesn’t stabilise the bullet but allows for it to wobble from side to side or even turn crosswise. In this case, shoot paper targets to check that the holes are round and the accuracy is good enough for your purpose.
|
Extreme examples
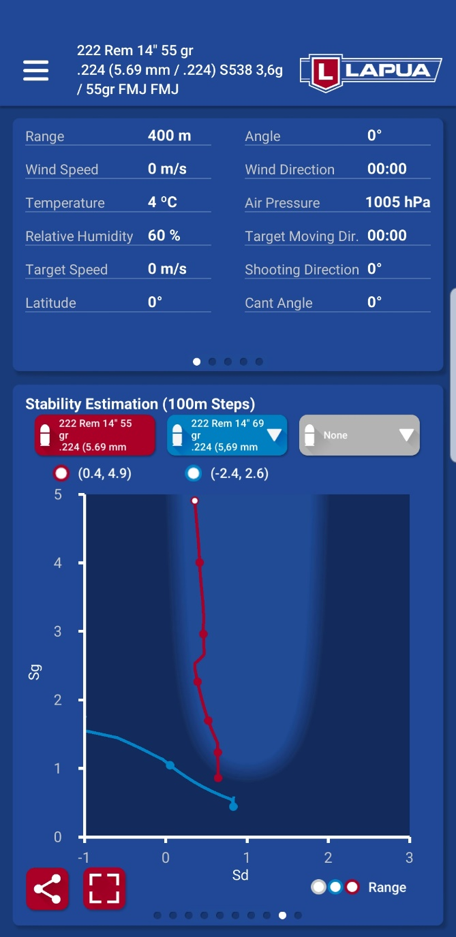
In this graph you can see two .222 Rem. caliber bullets, both shot with a 1:14” twist rate rifle.
- The .222 Rem is designed for short 55 gr FMJ-bullets (red curve). Even if the gyroscopic stability is dangerously low in the beginning (ca. 1.0), it increases rapidly and this short flat base bullet is not susceptible to wobbling. This combination is in practise a well-proven small game cartridge.
- The 69 gr Scenar bullet (blue curve) is much too long for this twist rate. Gyroscopic stability starts from a very low value and also the dynamic stability starts to weaken significantly immediately. This bullet will likely not be stabilized at all and the accuracy potential is very low and likely the holes in a paper target are oval – even at 100 m/yds.
|
Temporary loss of stability
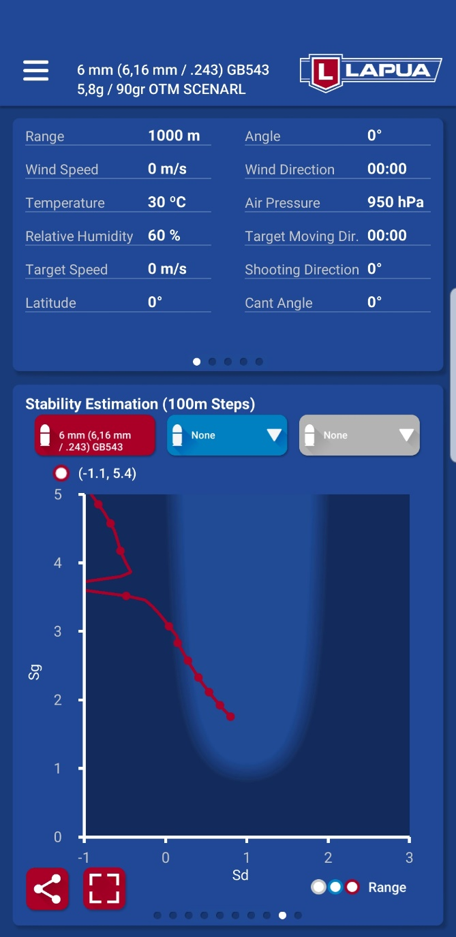
| In this graph you can see a temporary loss of stability at a distance of 650 – 850 m/yds with a 6 mm 90 gr GB543 Scenar bullet. In this case the projectile reaches the transonic area at the distance of 700 m. Stability will revert soon after that and the bullet likely continues a stable flight without a loss of accuracy. This is also helped by the high gyroscopic stability value of over 3.5. |
Lapua Ballistics 6 DOF is the only free of charge consumer software capable for these kind of studies. For those interested to understand the theory behind bullet stability even further, we recommend the following reading:
- McCoy, R. Modern Exterior Ballistics, the Launch and Flight Dynamics of Symmetric Projectiles. Schiffer Publishing, 1999
- Bryan Litz, Applied Ballistics For Long Range Shooting 3rd Edition
- Sailaranta, T. Studies on Unmanned Atmospheric Flight. Doctoral Thesis. Aalto-University, Helsinki, Finland.
Our next tip will feature the use of spin drift adjustment. Stay tuned!
Go to Lapua Ballistics main page
Back to news and updates















